【【草稿】】分子振动

振动模式

• 一个拥有 n 个原子的非线性分子有 3n − 6 个振动正交模（vibrational normal mode），其余为 3 个转动、3 个移动。而线性的分子有 3n − 5 个振动正交模，只有 2 个转动。
  • 原因：当所有原子都沿着x或y或z方向移动的时候，只是整个分子在移动，而不是分子在振动，因此要减去3个自由度；而当所有原子沿着x或y或z方向转动时，也不是分子振动，因此要再减去3个自由度（当线性的时候，没有分子轴的转动，所以是减去2）。

振动模式的分类

对称伸缩 （Symmetrical stretching）	不对称伸缩 （Asymmetrical stretching）	平面剪式运动 （Scissoring / Bending）
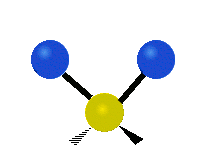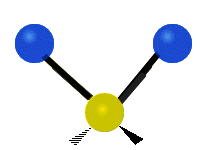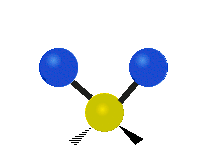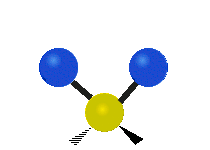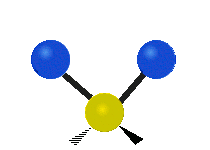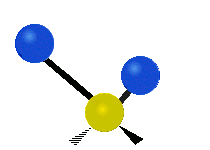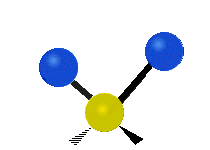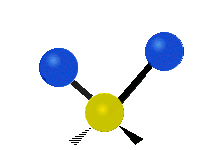平面摆动 （Rocking）	非平面摇摆 （Wagging）	非平面扭转 （Twisting）

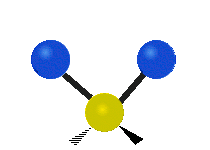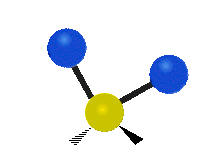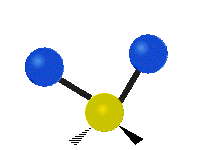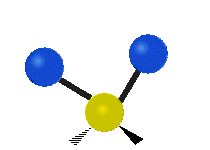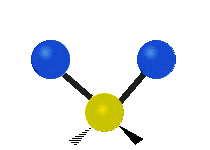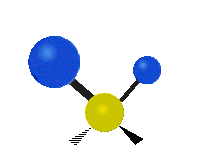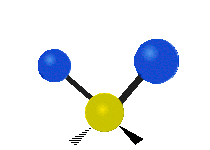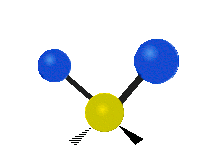• 在摆动、摇摆与扭转模，原子间的键长不会改变。

举例

牛顿力学

• 将振动看作弹簧，则在谐波近似（harmonic approximation）中，服从胡克定律（Hooke’s law）：拉伸弹簧所需的力与拉伸量成正比：$F=-kQ$（k是力常数，单位为N/cm=dyn/cm）

• 牛顿第二定律：$F=ma=\mu \frac{d^{2} Q}{d t^{2}}$（$\mu$是约化质量，单位为g，一般来说，双原子为$\frac{1}{\mu}=\frac{1}{m_{A}}+\frac{1}{m_{B}}$）

• 联立以上两个方程，可以解得：（A是最大振幅）

  $$Q(t)=A \cos (2 \pi \nu t) ; \quad \nu=\frac{1}{2 \pi} \sqrt{\frac{k}{\mu}}$$
  • 当用相对原子质量计算，频率用波数（$cm^{-1}$）时，可以得到$\tilde{v}=\frac{v}{c}=1307 \sqrt{\frac{k}{A}}$

• 在谐波近似中，力常数是势能的二阶导：$k=\frac{\partial^{2} V}{\partial Q^{2}}$

量子力学

• 动能算符：$\frac{p^{2}}{2m}$（$p=-i \hbar \frac{d}{d x}$）

• 薛定谔方程：$-\frac{h^{2}}{8 \pi^{2} \mu_{A B}} \frac{d^{2} \psi}{d x^{2}}+\frac{1}{2} k x^{2} \psi=E \psi$，解方程得到（n为量子数，取0，1，2……）：

  $$E_{n}=h\left(n+\frac{1}{2}\right) \nu=h\left(n+\frac{1}{2}\right) \frac{1}{2 \pi} \sqrt{\frac{k}{m^{\prime}}}$$

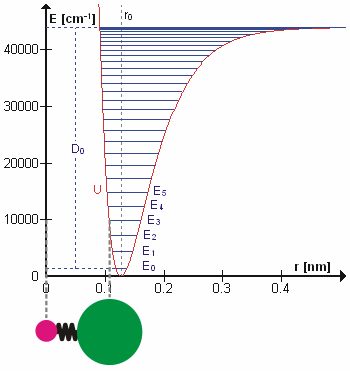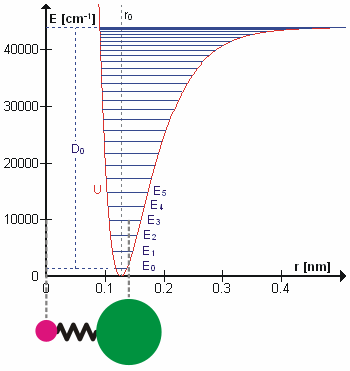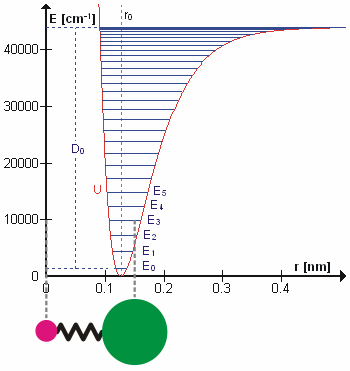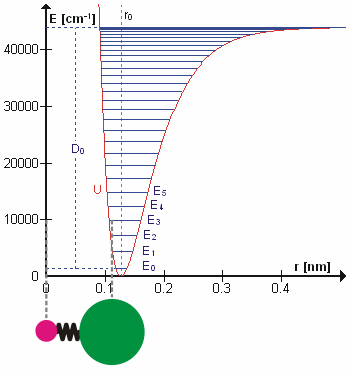
• 当n变化时，能量变化为hv。
• 当分子吸收能量ΔE时，分子振动被激发，对应于振动的频率ν，根据关系ΔE = hν。当一个这样的能量量子被处于基态的分子吸收时，就会引发基本振动。

群论的应用

以$D_{3h}$点群的碳酸根$CO_3^-$为例，一共有3n-3=6种正则振动。

这些振动方式的对称都是属于某一个不可约表示：

• 对于$v_1$，所有对称操作都没有改变图中的箭头（向量），全是1，因此是$A^{\prime}_1$对称性
• 对于$v_2$，$E$，$C_3$和$\sigma_v$不会改变向量，而$C_2$，$\sigma_h$和$S_3$则变为负，因此符合$A^{\prime\prime}_2$
• 对于$v_3$复杂一些，需要用$v_{3a}$和$v_{3b}$共同表示：
  • 对于$E$，$E\left(v_{3 a}\right)=v_{3 a}+0 v_{3 b} $，$E\left(v_{3 b}\right)=0 v_{3 a}+v_{3 b}$，用矩阵表示$\left[\begin{array}{ll}1 & 0 \\0 & 1\end{array}\right]$，则特征标为2；
  • 对于$C_3$，如下图：$C_{3}\left(v_{3 a}\right)=-\frac{1}{2} v_{3 a}+\frac{1}{2} v_{3 b}$，$C_{3}\left(v_{3 b}\right)=-\frac{3}{2} v_{3 a}-\frac{1}{2} v_{3 b}$，则为$\left[\begin{array}{rr}-\frac{1}{2} & \frac{1}{2} \\-\frac{3}{2} & -\frac{1}{2}\end{array}\right]$，特征标为-1
  • 其他以此类推，符合$E^{\prime\prime}$

确定正则振动的对称性

1. 通过给每个原子一个独立的笛卡尔坐标系，以该原子为原点，所有的x，y，z轴方向都相同，如下图：
   

2. 用每一个对称操作作用在这个分子上，用变换前的坐标表示变换后的坐标，比如$C_3$：

   

• 则：$X_{1}^{’}=-\frac{1}{2} X_{2}-\left(\frac{\sqrt{3}}{2}\right) Y_{2}$，可以得到特征标为0的矩阵：

• 对于$E$操作，对角线全是1，特征标为12。

• 更加简单的看是，只需要考虑没有移动到别的原子上的笛卡尔坐标系。因为它们处于对角线上。比如$X_{1}$，$Y_{1}$，$Z_{1}$在$C_3$都旋转到原子2上了，因此可以不用考虑。而原子4上的坐标仍然在原子4上，因此可以直接看原子4上的变换矩阵（红框部分）。

  • 对于$C_2$操作绕着X轴旋转，只有原子1和原子4的坐标没有移走，而且X向量不发生改变，Z和Y分别变成负的，则特征标的数值为$(1-1-1)\times2=-2$
  • 对于$\sigma_h$，每个原子都只有一个向量变成负的，则为$(1+1-1)\times4=4$
  • 对于$S_3$，则是先$C_3$后再$\sigma_h$，所以就是$-1/2-1/2-1=2$
  • 对于$\sigma_v$，两个原子不变，每个原子有一个向量变成负的，因此特征标为2

1. 得到12个笛卡尔坐标产生的特征标后，进行分解：

   

$$\Gamma_{i}=A_{1}^{\prime}+A_{2}^{\prime}+3 E^{\prime}+2 A_{2}^{\prime \prime}+E^{\prime \prime}$$

1. 扣除6个移动和转动，通过上表可以得知，跟x，y，z移动相关的为$E^{\prime}$和$A_{2}^{\prime \prime}$，与x，y，z转动相关的是$A_{2}^{\prime}$和$E^{\prime\prime}$，进行扣除： $$\Gamma_{g}=A_{1}^{\prime}+2E^{\prime}+A_{2}^{\prime \prime}$$

通过内坐标看正则振动的贡献

1. 选择三个C-O键的伸缩作为内坐标组，则特征标的顺序是3 0 1 3 0 1，进行分解可以得到$A_{1}^{\prime}+E^{\prime}$，可以看出这两个振动方式包含一定程度的C-O振动。（也可以通过羰基六种正则振动的图验证，与C-O键伸缩振动相关的是$A_{1}^{\prime}+E^{\prime}$）
2. 选择三个OCO键角作为第二组内坐标组：
   • 首先要注意所有坐标不是线性无关的。如果振动使得三个OCO键角同时增大或减小，振动是$A_{1}^{\prime}$的对称性，但是这三个角在一个平面内不可能同时增大或减小，因此这个对称性是与键角的振动无关的。
   • 同样按对称操作，则得到3 0 1 3 0 1，分解得到也是$A_{1}^{\prime}+E^{\prime}$，但是$A_{1}^{\prime}$的振动是冗余的要去掉
   • 因此$E^{\prime}$的振动包含一定的OCO角的弯曲
3. 还剩一个$A_{2}^{\prime\prime}$，因此它是与二面角有关的，即C-O键与离子平面间所成的角有变化，不包含C-O键长和平面内OCO键角的变化。

判断红外和拉曼活性

• 红外偶极辐射的吸收发生基频跃迁必须包含一个或多个非零的$\int \psi_{\nu}^{0} x \psi_{\nu}^{j} d \tau$，$\int \psi_{\nu}^{0} y \psi_{\nu}^{j} d \tau$，$\int \psi_{\nu}^{0} z \psi_{\nu}^{j} d \tau$积分，这些积分与x，y，z有关。
• 拉曼散射至少需要一个非零的$\int \psi_{\nu}^{0} P \psi_{\nu}^{j} d \tau$，$P$是笛卡尔坐标的二元函数，即与$x^2$，$y^2$，$z^2$，xy，yz，zx有关
• 因此通过特征标表，可知$D_{3h}$点群的振动$\Gamma_{g}=A_{1}^{\prime}+2E^{\prime}+A_{2}^{\prime \prime}$中：
  • 只具有拉曼活性：$A_{1}^{\prime}$和$E^{\prime\prime}$
  • 只具有红外活性：$A_{2}^{\prime\prime}$
  • 都有：$E^{\prime}$